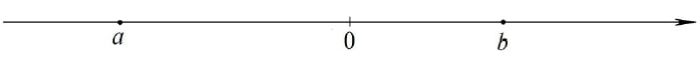ВПР. Математика. 8 класс. Вариант — 1
Код
Проверочная работа
по МАТЕМАТИКЕ
8 класс
Вариант — 1
Инструкция по выполнению работы
На выполнение работы по математике даётся 90 минут. Работа
содержит 19 заданий.
В заданиях, после которых есть поле со словом «Ответ», запишите
ответ в указанном
месте.
В заданиях, после которых есть поле со словами «Решение» и
«Ответ», запишите
решение
и ответ в указанном месте.
В заданиях 4 и 8 нужно отметить точки на числовой прямой.
Если Вы хотите изменить ответ, зачеркните его и запишите рядом
другой.
При выполнении работы можно пользоваться таблицей умножения и
таблицей
квадратов
двузначных чисел. Запрещено пользоваться учебниками, рабочими тетрадями,
справочниками,
калькулятором.
При необходимости можно пользоваться черновиком. Записи в
черновике проверяться
и
оцениваться не будут.
Советуем выполнять задания в том порядке, в котором они даны.
Для экономии
времени
пропускайте задание, которое не удаётся выполнить сразу, и переходите
к
следующему. Постарайтесь выполнить как можно больше заданий.
Желаем успеха!
©
2020 Федеральная служба по надзору в сфере образования и науки
ВПР. Математика. 8 класс. Вариант — 1
Код
1. Найдите
значение выражения
|
Ответ: |
||||||||||||||||||||||||
ИЛИ
Найдите значение выражения
|
Ответ: |
||||||||||||||||||||||||
2. Решите уравнение
|
Ответ: |
||||||||||||||||||||||||
3.
Площадь земель крестьянского хозяйства, отведённая под посадку
сельскохозяйственных культур, составляет 63 га и распределена
между зерновыми и бахчевыми культурами в отношении 4:5. Сколько
гектаров занимают зерновые культуры?
|
|
||||||||||||||||||||||||
4. На координатной прямой отмечены числа a
и b . Отметьте на прямой какую-нибудь точку x так, чтобы при
этом выполнялись три условия:
Ответ:
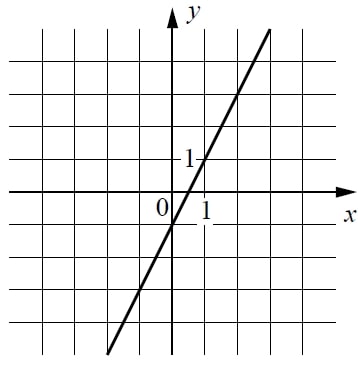
5. На рисунке изображён график линейной функции.
Напишите формулу,
которая задаёт эту линейную функцию,
если коэффициент
перед переменной .
|
Ответ: |
|||||||||||||||||||
©
2020 Федеральная служба по надзору в сфере образования и науки
ВПР. Математика. 8 класс. Вариант — 1
Код
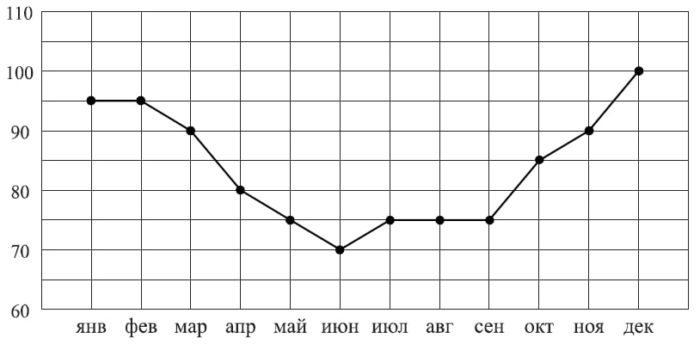
6. На графике показан процесс разогрева двигателя
легкового автомобиля. На
оси абсцисс откладывается время в минутах, прошедшее от запуска
двигателя,
на оси ординат — температура двигателя в градусах
Цельсия. Определите по
графику, сколько минут двигатель нагревался до температуры
50 °C с момента
запуска двигателя. На сколько градусов больше нагрелся
двигатель до
максимальной температуры считая от момента нагрева 50
В ответе запишите
числа через точку с запятой.
|
|
||||||||||||||||||||||||
7.
В таблице приведены результаты двух полуфинальных
забегов на дистан-
цию 60 м. В финальном забеге 6 участников. Из каждого
полуфинала в финал
выходят два спортсмена, показавших первый и второй
результаты. К ним до-
бавляют еще двух спортсменов, показавших лучшее время
среди всех осталь

Запишите в ответ номера спортсменов, не попавших в финал.
|
|
||||||||||||||||||||||||
©
2020 Федеральная служба по надзору в сфере образования и науки
ВПР. Математика. 8 класс. Вариант — 1
Код
8. Отметьте на
координатной прямой числа и
.
Ответ:
9. Найдите значение выражения
при
|
Ответ: |
||||||||||||||||||||||||
10. На конкурсе танцев выступают группы — по одной от
каждой из заявленных городов страны, среди этих городов Москва, Нижний
Новгород и Ярославль. Порядок выступления определяется жребием.
Какова вероятность того, что группа из Нижнего
Новгорода будет выступать до группы из Москвы, но после группы из
Ярославля?
|
Ответ: |
||||||||||||||||||||||||
11. Свежие фрукты содержат 80%
воды, а высушенные — 28%. Сколько требуется свежих фруктов для
приготовления 80 кг высушенных фруктов?
|
|
||||||||||||||||||||||||
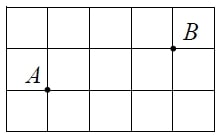
12 На клетчатой бумаге с размером клетки 1см x 1см отмечены
точки А, В и С.

середины отрезка ВС.
Ответ
выразите в сантиметрах.
|
|
||||||||||||||||||||||||
© 2020
Федеральная служба по надзору в сфере образования и науки
ВПР. Математика. 8 класс. Вариант —
1 Код
13.
Точка H является основанием высоты, проведённой из вершины
прямого угла B треугольника ABC к гипотенузе AC.
Найдите AB, если AH = 6, AC = 24.
|
|
||||||||||||||||||||||||
14.
Укажите номер верного утверждения.
1)
Если два угла
треугольника равны, то равны и противолежащие им стороны.
2)
Если
угол острый, то смежный с ним угол также является острым.
3)
Любая высота
равнобедренного треугольника является его биссектрисой.
4) Если угол равен 45°, то вертикальный с ним угол
равен 45°.
Если утверждений несколько, запишите
их номера в порядке возрастания.
|
|
||||||||||||||||||||||||
15.
Окружность,
вписанная в треугольник ABC , касается его сторон в
точках M, K и P. Найдите углы треугольника ABC,
если углы треугольника MKP равны 49°, 69° и 62°.
В ответ запишите величину углов через запятую в порядке
возрастания.
|
Решение: |
|||||||||||||||||||||||||||||
© 2020
Федеральная служба по надзору в сфере образования и науки
ВПР. Математика. 8 класс. Вариант —
1 Код
|
Ответ: |
|||||||||||||||||||||||||||||
16.
На графиках показано, как
во время телевизионных дебатов между кандидатами А и Б телезрители
голосовали за каждого из них. Сколько всего телезрителей проголосовало
к 20-й минуте дебатов?
|
|
||||||||||||||||||||||||
© 2020
Федеральная служба по надзору в сфере образования и науки
ВПР. Математика. 8 класс. Вариант —
1 Код
17.
В треугольнике АВС углы А и С равны
40° и 60° соответственно. Найдите угол между высотой ВН и
биссектрисой BD.
 |
|
Решение: |
|||||||||||||||||||||||||||||
|
Ответ: |
|||||||||||||||||||||||||||||
© 2020 Федеральная
служба по надзору в сфере образования и науки
ВПР. Математика. 8 класс. Вариант —
1 Код
18.
Запишите
решение и ответ.
|
Решение: |
|||||||||||||||||||||||||||||
|
Ответ: |
|||||||||||||||||||||||||||||
© 2020
Федеральная служба по надзору в сфере образования и науки
ВПР. Математика. 8 класс. Вариант — 2
Код
Проверочная работа
по МАТЕМАТИКЕ
8 класс
Вариант — 2
Инструкция по выполнению работы
На выполнение работы по математике даётся 90 минут. Работа
содержит 19 заданий.
В заданиях, после которых есть поле со словом «Ответ», запишите
ответ в указанном
месте.
В заданиях, после которых есть поле со словами «Решение» и
«Ответ», запишите
решение
и ответ в указанном месте.
В заданиях 4 и 8 нужно отметить точки на числовой прямой.
Если Вы хотите изменить ответ, зачеркните его и запишите рядом
другой.
При выполнении работы можно пользоваться таблицей умножения и
таблицей
квадратов
двузначных чисел. Запрещено пользоваться учебниками, рабочими тетрадями,
справочниками,
калькулятором.
При необходимости можно пользоваться черновиком. Записи в
черновике проверяться
и
оцениваться не будут.
Советуем выполнять задания в том порядке, в котором они даны.
Для экономии
времени
пропускайте задание, которое не удаётся выполнить сразу, и переходите
к
следующему. Постарайтесь выполнить как можно больше заданий.
Желаем успеха!
©
2020 Федеральная служба по надзору в сфере образования и науки
ВПР. Математика. 8 класс. Вариант — 2
Код
1. Найдите
значение выражения
|
Ответ: |
||||||||||||||||||||||||
ИЛИ
Найдите значение выражения
|
Ответ: |
||||||||||||||||||||||||
2. Решите уравнение
|
Ответ: |
||||||||||||||||||||||||
3.
Площадь
земель крестьянского хозяйства, отведённая под посадку сельскохозяйственных
культур, составляет 36 га и распределена между зерновыми и овощными
культурами в отношении 2:7 . Сколько гектаров занимают овощные
культуры?
|
Ответ: |
||||||||||||||||||||||||
На координатной
прямой отмечены числа a и b . Отметьте на прямой какую-
4. нибудь
точку x так, чтобы при этом выполнялись три условия:
© 2020
Федеральная служба по надзору в сфере образования и науки
ВПР. Математика. 8 класс. Вариант — 2
Код
5. На рисунке изображён график линейной функции.
Напишите формулу,
которая задаёт эту линейную функцию,
если коэффициент
перед переменной .
|
Ответ: |
|||||||||||||||||||
6. На графике представлена динамика изменения
курса доллара США в рублях
за период с 19 ноября по 19 декабря. По горизонтальной
оси отложены даты,
по вертикальной — значения доллара США. Шаг по вертикальной
оси равен
0,0372 руб. Определите по графику, каким был курс доллара
США к рублю
21 ноября. На сколько рублей курс доллара США был
выше 21 ноября,
чем через две недели.
В ответе запишите
числа через точку с запятой.
|
Ответ: |
||||||||||||||||||||||||
© 2020
Федеральная служба по надзору в сфере образования и науки
.
ВПР. Математика. 8 класс. Вариант — 2
Код
7.
В таблице
приведены размеры штрафов за превышение максимальной
разрешённой скорости, зафиксированное с помощью
средств автоматической
фиксации, установленных на территории России на 1 января
2013 года.
Какой штраф должен заплатить
владелец автомобиля, зафиксированная скорость которого составила
175 км/ч на участке дороги с максимальной разрешённой скоростью 110
км/ч?
|
|
||||||||||||||||||||||||
8.
Отметьте на координатной прямой числа и
.
Ответ:
9. Найдите значение выражения
при
|
Ответ: |
||||||||||||||||||||||||
10. В соревнованиях по художественной гимнастике
участвуют группы
гимнасток из России, Украины, Белоруссии и Китая.
Порядок выступлений определяется жеребьёвкой.
Найдите вероятность того, что группа гимнасток из России
будет выступать
до группы из Белоруссии, но после группы из Китая.
|
Ответ: |
||||||||||||||||||||||||
© 2020
Федеральная служба по надзору в сфере образования и науки
ВПР. Математика. 8 класс. Вариант — 2
Код
11.
Свежие фрукты содержат 93% воды, а высушенные
— 16%.
Сколько
сухих фруктов получится из 252 кг свежих фруктов?
|
|
||||||||||||||||||||||||

клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С.
Найдите расстояние от точки А до середины отрезка ВС.
Ответ выразите в сантиметрах.
|
Ответ: |
||||||||||||||||||||||||
13.
Точка H является
основанием высоты, проведённой из вершины прямого угла B треугольника ABC к
гипотенузе AC. Найдите BС, если HС = 3, AC = 12.
|
|
||||||||||||||||||||||||
14. Какие
из следующих утверждений верны?
1) Если
при пересечении двух прямых третьей прямой внутренние накрест лежащие
углы составляют в сумме 90°, то эти две прямые параллельны.
2) Если
угол равен 60°, то смежный с ним равен 120°.
3) Если
при пересечении двух прямых третьей прямой внутренние односторонние
углы равны 70° и 110°, то эти две прямые параллельны.
4) Через
любые три точки проходит не более одной прямой.
Если утверждений несколько, запишите
их номера в порядке возрастания.
|
Ответ: |
||||||||||||||||||||||||
© 2020
Федеральная служба по надзору в сфере образования и науки
ВПР. Математика. 8 класс. Вариант — 2
Код
15.
Окружность пересекает стороны AB и AC треугольника ABC в
точках K и P соответственно и проходит
через вершины B и C. Найдите длину отрезка KP,
если AK = 18, а сторона AC в 1,2 раза
больше стороны BC.
|
Решение: |
|||||||||||||||||||||||||||||
|
Ответ: |
|||||||||||||||||||||||||||||
© 2020
Федеральная служба по надзору в сфере образования и науки
ВПР. Математика. 8 класс. Вариант — 2
Код
16.
На графиках показано, как во время телевизионных
дебатов между кандидатами А и Б телезрители голосовали за каждого
из них. Сколько всего тысяч телезрителей проголосовало за первые 50 минут
дебатов?
|
Ответ: |
||||||||||||||||||||||||
17.
В треугольнике АВС углы А и С равны
30° и 50° соответственно. Найдите угол между высотой ВН и
биссектрисой BD.
 |
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
© 2020
Федеральная служба по надзору в сфере образования и науки
ВПР. Математика. 8 класс. Вариант — 2
Код
|
Ответ: |
|||||||||||||||||||||||||||||
18.
|
Решение: |
||||||||||||||||||||||||||||
© 2020
Федеральная служба по надзору в сфере образования и науки
ВПР. Математика. 8 класс. Вариант — 2
Код
|
Ответ: |
||||||||||||||||||||||||||||
©
2020 Федеральная служба по надзору в сфере образования и науки
ВПР. Математика. 8 класс. Вариант —
2 Код
Система оценивания проверочной работы
Оценивание отдельных заданий
|
Задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
Итого |
|
Баллы |
1 |
1 |
1 |
1 |
1 |
2 |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
1 |
2 |
2 |
2 |
25 |
Ответы В-1
|
Номер задания |
Правильные ответы |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
3 |
|
7 |
38 |
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
288 кг |
|
12 |
4 |
|
13 |
12 |
|
14 |
14 |
|
15 |
42; 56; 82 |
|
16 |
25 000 |
|
17 |
10 |
|
18 |
12,5 |
№ 7.
Решение.
В первом полуфинале два лучших времени
показали спортсмены 1 и 4, во втором — спортсмены 6 и 7. Среди всех остальных
участников полуфинала два наилучших времени показали спортсмены 2 и 5.
Следовательно, в финал не попадут спортсмены 3 и 8.
Ответ: 38.
№11.
Решение.
Заметим, что сухая часть свежих фруктов
составляет 20%, а высушенных — 72%. Значит, для приготовления 80 кг высушенных
фруктов требуется кг свежих.
Ответ: 288 кг.
©
2020 Федеральная служба по надзору в сфере образования и науки
ВПР. Математика. 8 класс. Вариант —
2 Код
№13.
Решение.
Рассмотрим
треугольники и
они — прямоугольные, угол
— общий, следовательно, треугольники подобны. Откуда:
Ответ: 12.
№15
Решение.
По свойству угла между касательной и хордой
т.е.
.
Т.к.
;
Из
.
По аналогии находим
Ответ:42; 56
; 82
№16.
Решение.
К 20-й минуте дебатов за кандидата А
проголосовали 15 тыс. человек, а за кандидата Б — 10 тыс. человек.
Всего проголосовало 15 + 10 = 25 тыс. чел.

№17.
Решение.
Из треугольника найдем ∠
— биссектриса, следовательно,
Треугольник — прямоугольный, следовательно:
Найдём угол
Ответ: 10°.
ВПР. Математика. 8 класс. Вариант —
2 Код
Ответы В-2
|
Номер задания |
Правильные ответы |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
31,4218 и |
|
7 |
2500 руб. |
|
8 |
|
|
9 |
|
|
10 |
0,3 |
|
11 |
21 |
|
12 |
5 |
|
13 |
6 |
|
14 |
|
|
15 |
15 |
|
16 |
65 |
|
17 |
10 |
|
18 |
8 |
№7
Решение.
Найдём превышение скорости автомобиля: 175
− 110 = 65 км/ч. Из таблицы находим,что такому превышению скорости
соответствует штраф в размере 2500 рублей.
Ответ: 2500 руб..
№10.
Решение.
Всего в соревнованиях участвуют 3 + 3 + 4
= 10 гимнасток. Поэтому вероятность того, что первой будет выступать гимнастка
из России равна
Ответ: 0,3.
№11.
Решение.
Свежие фрукты содержат 7% питательного
вещества, а высушенные — 84%. В 252 кг свежих фруктов содержится
0,07 · 252 = 17,64 кг питательного вещества. Такое
количество питательного вещества будет содержаться в кг высушенных фруктов.
Ответ: 21.
© 2020
Федеральная служба по надзору в сфере образования и науки
ВПР. Математика. 8 класс. Вариант —
2 Код
№15.
Решение.
Поскольку
четырёхугольник вписан в окружность, сумма противоположных углов
равна180°,следовательно, Углы
и
—смежные, следовательно,
Из приведённых равенств, получаем, что
Рассмотрим треугольники
и
угол
— общий, углы
и
равны, следовательно, треугольники подобны, откуда
Используя равенство найдём
Ответ: 15.
№16.
Решение.
К 50-й минуте дебатов за кандидата А
проголосовали 30 тыс. человек, а за кандидата Б — 35 тыс. человек.
Всего проголосовало 30 + 35 = 65 тыс. чел.
Ответ: 65.
№17.
Решение.
Из треугольника найдем
— биссектриса, следовательно,
Треугольник — прямоугольный, следовательно:
Найдём угол
Ответ: 10°.
Система оценивания выполнения всей работы
Максимальный балл за выполнение работы — 25.
Рекомендации по переводу первичных баллов
в отметки по пятибалльной шкале
|
Отметка по пятибалльной шкале |
«2» |
«3» |
«4» |
«5» |
|
Первичные баллы |
0-7 |
8-14 |
15—20 |
21-25 |
© 2020
Федеральная служба по надзору в сфере образования и науки
Расписание ВПР−2023
| Период проведения | Класс | Учебный предмет | Примечание |
|---|---|---|---|
| С 15 марта по 20 мая | 4 | Русский язык | В штатном режиме. ВПР по конкретным предметах проводятся во всех классах данной параллели. |
| Математика | |||
| Окружающий мир | |||
| 5 | Русский язык | ||
| Математика | |||
| История | |||
| Биологи | |||
| 6 | Русский язык | ||
| Математика | |||
| 4, 5, 6 | Русский язык, математика |
В штатном режиме. |
|
| 7 | Русский язык | В штатном режиме. ВПР по конкретным предметам проводятся во всех классах данной параллели. |
|
| Математика | |||
| 8 | Русский язык | ||
| Математика | |||
| 7, 8 | Математика, Физика (с углубленным изучением предмета) |
В штатном режиме. ВПР проводятся в классах с углубленным изучением предмета данной параллели. | |
| 7 | Английский язык | В штатном режиме. ВПР проводятся во всех классах данной параллели. |
|
| Немецкий язык | |||
| Французский язык | |||
| 6 | История | В штатном режиме. ВПР в параллели 6, 7, 8 классов проводятся для каждого класса по двум предметам на основе случайного выбора. Информация о распределении предметов по классам в параллели предоставляется в образовательную организацию через личный кабинет в Федеральной информационной системе оценки качества образования. |
|
| Биология | |||
| География | |||
| Обществознание | |||
| 7 | История | ||
| Биология | |||
| География | |||
| Обществознание | |||
| Физика | |||
| 8 | История | ||
| Биология | |||
| География | |||
| Обществознание | |||
| Физика | |||
| Химия | |||
| С 4 апреля по 17 апреля | 5, 6, 7, 8 | История | В штатном режиме. При проведении ВПР предоставляется альтернативная возможность выполнения участниками работ в компьютерной форме. |
| Биология | |||
| География | |||
| Обществознание | |||
| 18 апреля | 5, 6, 7, 8 | История | Резервный день для выполнения участниками работ в компьютерной форме. |
| Биология | |||
| География | |||
| Обществознание | |||
| С 1 марта по 25 марта | 10 | География | В режиме апробации. |
| С 1 марта по 25 марта | 11 | История | В режиме апробации. |
| Биология | |||
| География | |||
| Физика | |||
| Химия | |||
| Английский язык | |||
| Немецкий язык | |||
| Французский язык | |||
| 11 | Единая проверочная работа по социально-гуманитарным предметам | В режиме апробации. Выборочное проведение ВПР с контролем объективности результатов. |
Приказ Рособрнадзора.
НАЗНАЧЕНИЕ ВСЕРОССИЙСКОЙ ПРОВЕРОЧНОЙ РАБОТЫ
Назначение КИМ для проведения проверочной работы по математике — оценить качество общеобразовательной подготовки обучающихся 8 классов в соответствии с требованиями ФГОС.
СТРУКТУРА И СОДЕРЖАНИЕ ВСЕРОССИЙСКОЙ ПРОВЕРОЧНОЙ РАБОТЫ
Работа содержит 19 заданий.
В заданиях 1–3, 5, 7, 9–14 необходимо записать только ответ.
В заданиях 4 и 8 нужно отметить точки на числовой прямой.
В задании 6 требуется записать обоснованный ответ.
В задании 16 требуется дать ответ в пункте 1 и схематично построить график в пункте 2.
В заданиях 15, 17–19 требуется записать решение и ответ.
ОБОБЩЁННЫЙ ПЛАН ВАРИАНТА ВПР ПО МАТЕМАТИКЕ
Всего заданий — 19, из них по уровню сложности: Б — 12, П — 6, В — 1.
Максимальный балл за работу — 25 баллов.
Общее время выполнения работы — 90 мин.
РАСПРЕДЕЛЕНИЕ ЗАДАНИЙ ВАРИАНТА ПРОВЕРОЧНОЙ РАБОТЫ ПО СОДЕРЖАНИЮ, ПРОВЕРЯЕМЫМ УМЕНИЯМ И ВИДАМ ДЕЯТЕЛЬНОСТИ
В задании 1 проверяется владение понятиями «отрицательное число», «обыкновенная дробь», «десятичная дробь», вычислительными навыками.
В задании 2 проверяется умение решать линейные, квадратные уравнения, а также системы уравнений.
В задании 3 проверяется умение решать задачи на части.
В задании 4 проверяется знание свойств целых чисел и правил арифметических действий.
Задание 5 проверяет владение понятиями «функция», «график функции», «способы задания функции».
Задание 6 направлено на проверку умения извлекать и анализировать информацию, представленную в таблицах, на диаграммах, графиках.
В задании 7 проверяются умения читать информацию, представленную в таблицах, на диаграммах, графиках и определять статистические характеристики данных.
В задании 8 проверяется умение сравнивать действительные числа.
В задании 9 проверяется умение выполнять преобразования буквенных дробно-рациональных выражений.
Задание 10 направлено на проверку умения в простейших случаях оценивать вероятность события.
Задание 11 проверяет умение решать текстовые задачи на проценты, в том числе задачи в несколько действий.
Задания 12–15 и 17 проверяют умение оперировать свойствами геометрических фигур, а также знание геометрических фактов и умение применять их при решении практических задач.
В задании 16 проверяются умения извлекать из текста необходимую информацию, представлять данные в виде диаграмм, графиков.
Задание 18 направлено на проверку умения решать текстовые задачи на производительность, движение.
Задание 19 является заданием высокого уровня сложности и направлено на проверку логического мышления, умения проводить математические рассуждения.
| № задания |
Умения, виды деятельности (в соответствии с ФГОС) |
Блоки ПООП ООО выпускник научится / получит возможность научиться |
Уровень сложности
|
Максимальный балл за выполнение задания |
Примерное время выполнения задания обучающимся (в минутах) |
| 1 | Развитие представлений о числе и числовых системах от натуральных до действительных чисел |
Оперировать на базовом уровне понятиями «обыкновенная дробь», «смешанное число», «десятичная дробь» |
Б | 1 | 2 |
| 2 | Овладение приёмами решения уравнений, систем уравнений |
Оперировать на базовом уровне понятиями «уравнение», «корень уравнения»; решать линейные и квадратные уравнения / решать квадратные уравнения и уравнения, сводимые к ним с помощью тождественных преобразований |
Б | 1 | 2 |
| 3 | Развитие умений применять изученные понятия, результаты, методы для задач практического характера и задач из смежных дисциплин |
Составлять числовые выражения при решении практических задач |
Б | 1 | 3 |
| 4 | Развитие представлений о числе и числовых системах от натуральных до действительных чисел |
Знать свойства чисел и арифметических действий |
Б | 1 | 3 |
| 5 | Овладение системой функциональных понятий, развитие умения использовать функционально-графические представления |
Строить график линейной функции |
Б | 1 | 3 |
| 6 | Развитие умения применять изученные понятия, результаты, методы для задач практического характера и задач из смежных дисциплин, умения извлекать информацию, представленную в таблицах, на диаграммах, графиках |
Читать информацию, представленную в виде таблицы, диаграммы, графика; использовать графики реальных процессов и зависимостей для определения их свойств / извлекать, интерпретировать информацию, представленную в таблицах и на диаграммах, отражающую свойства и характеристики реальных процессов и явлений |
П | 2 | 6 |
| 7 | Умения извлекать информацию, представленную в таблицах, на диаграммах, графиках, описывать и анализировать массивы данных с помощью подходящих статистических характеристик |
Читать информацию, представленную в виде таблицы, диаграммы, графика | Б | 1 | 5 |
| 8 | Развитие представлений о числе и числовых системах от натуральных до действительных чисел |
Оценивать значение квадратного корня из положительного числа / знать геометрическую интерпретацию целых, рациональных, действительных чисел |
П | 2 | 5 |
| 9 | Овладение символьным языком алгебры |
Выполнять несложные преобразования дробно-линейных выражений, использовать формулы сокращённого умножения |
Б | 1 | 3 |
| 10 | Формирование представлений о простейших вероятностных моделях | Оценивать вероятность события в простейших случаях / оценивать вероятность реальных событий и явлений в различных ситуациях |
Б | 1 | 4 |
| 11 | Умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин |
Решать задачи на покупки; находить процент от числа, число по проценту от него, процентное отношение двух чисел, процентное снижение или процентное повышение величины |
Б | 1 | 4 |
| 12 | Овладение геометрическим языком, формирование систематических знаний о плоских фигурах и их свойствах, использование геометрических понятий и теорем |
Оперировать на базовом уровне понятиями геометрических фигур, извлекать информацию о геометрических фигурах, представленную на чертежах в явном виде, применять для решения задач геометрические факты |
Б | 1 | 3 |
| 13 | Овладение геометрическим языком, формирование систематических знаний о плоских фигурах и их свойствах, использование геометрических понятий и теорем |
Оперировать на базовом уровне понятиями геометрических фигур, применять для решения задач геометрические факты |
Б | 1 | 4 |
| 14 | Овладение геометрическим языком; формирование систематических знаний о плоских фигурах и их свойствах, использование геометрических понятий и теорем |
Оперировать на базовом уровне понятиями геометрических фигур, приводить примеры и контрпримеры для подтверждения высказываний |
Б | 1 | 4 |
| 15 | Развитие умений моделировать реальные ситуации на языке геометрии, исследовать построенную модель с использованием геометрических понятий и теорем, аппарата алгебры |
Использовать свойства геометрических фигур для решения задач практического содержания |
П | 2 | 6 |
| 16 | Развитие умения использовать функционально графические представления для описания реальных зависимостей |
Представлять данные в виде таблиц, диаграмм, графиков / иллюстрировать с помощью графика реальную зависимость или процесс по их характеристикам |
П | 2 | 8 |
| 17 | Овладение геометрическим языком, формирование систематических знаний о плоских фигурах и их свойствах, использование геометрических понятий и теорем |
Оперировать на базовом уровне понятиями геометрических фигур / применять геометрические факты для решения задач, в том числе предполагающих несколько шагов решения |
П | 1 | 6 |
| 18 | Развитие умения применять изученные понятия, результаты, методы для решения задач практического характера, умений моделировать реальные ситуации на языке алгебры, исследовать построенные модели с использованием аппарата алгебры |
Решать задачи разных типов (на производительность, движение) / решать простые и сложные задачи разных типов, выбирать соответствующие уравнения или системы уравнений для составления математической модели заданной реальной ситуации или прикладной задачи, выполнять оценку правдоподобия результатов |
П | 2 | 8 |
| 19 | Развитие умений точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить классификации, логические обоснования, доказательства |
Решать простые и сложные задачи разных типов, а также задачи повышенной трудности |
В | 2 | 10 |
СИСТЕМА ОЦЕНИВАНИЯ ОТДЕЛЬНЫХ ЗАДАНИЙ И РАБОТЫ В ЦЕЛОМ
Правильное решение каждого из заданий 1–5, 7, 9–14, 17 оценивается
1 баллом. Задание считается выполненным верно, если ученик дал верный
ответ: записал правильное число, правильную величину; изобразил
правильный рисунок.
Выполнение заданий 6, 8, 15, 16, 18, 19 оценивается от 0 до 2 баллов.
Рекомендации по переводу первичных баллов в отметки по пятибалльной шкале
| Отметка по пятибалльной шкале | «2» | «3» | «4» | «5» |
|---|---|---|---|---|
| Первичные баллы | 0–7 | 8–14 | 15–20 | 21–25 |
ДОПОЛНИТЕЛЬНЫЕ МАТЕРИАЛЫ И ОБОРУДОВАНИЕ
Дополнительные материалы и оборудование не требуются.
Решение и ответы заданий демонстрационного варианта ВПР 8 класс по математике. Образец всероссийской проверочной работы 2023 год.
Задание 1.
Найдите значение выражения
ИЛИ
Найдите значение выражения 4,5·5,4 – 6,1
Задание 2.
Решите уравнение (5х – 2)(–х + 3) = 0
Задание 3.
Площадь земель фермерского хозяйства, отведённых под посадку сельскохозяйственных культур, составляет 72 га и распределена между зерновыми и зернобобовыми культурами в отношении 7 : 2 соответственно. Сколько гектаров занимают зернобобовые культуры?
Задание 4.
На координатной прямой отмечены числа a и b. Отметьте на прямой какую-нибудь точку x так, чтобы при этом выполнялись три условия: x – a > 0, x – b < 0 и a2x > 0.
Задание 5.
На рисунке изображён график линейной функции. Напишите формулу, которая задаёт эту линейную функцию.
Задание 6.
Потребление электроэнергии измеряется в киловатт-часах ( кВт⋅ч). Жирными точками показано потребление электроэнергии в некоторой стране в течение 2016 года в миллиардах кВт⋅ч. Для наглядности точки соединены линиями. Данные округлены до 5 млрд кВт⋅ч.
На диаграмме видно, что потребление электроэнергии в середине года существенно ниже, чем в начале и конце года. Чем это можно объяснить? Можно ли предположить, в каком полушарии находится эта страна – в Южном или в Северном? Можно ли что-то сказать о том, суровые ли зимы в этой стране? Напишите два-три предложения, в которых кратко выскажите и обоснуйте своё мнение по этим вопросам.
Задание 7.
На соревнованиях по фигурному катанию каждый элемент имеет базовую стоимость и судейскую оценку. Девять судей независимо друг от друга выставляют за каждый элемент свои оценки от –5 до +5 баллов. Затем самая высокая и самая низкая оценки отбрасываются. Среднее арифметическое оставшихся семи оценок, округлённое до сотых, прибавляется к базовой стоимости. Полученная сумма является итоговой оценкой за элемент. Фигуристу Артёму Петрову судьи поставили оценки за три элемента. Эти оценки и базовая стоимость каждого элемента показаны в таблице. Определите, за какой элемент Артём Петров получил наиболее высокую оценку. В ответе запишите этот элемент и оценку за него.
Задание 8.
Отметьте на координатной прямой числа √10 и √34
Задание 9.
Найдите значение выражения при х = √3, y = –5,2.
Задание 10.
На фестивале выступают группы – по одной от каждой из заявленных стран, среди этих стран Румыния, Болгария и Греция. Порядок выступления определяется жребием. Какова вероятность того, что группа из Румынии будет выступать до группы из Болгарии, но после группы из Греции?
Задание 11.
Свежие абрикосы содержат 88% воды, а сушеные абрикосы (курага) – 30%. Сколько требуется свежих абрикосов для приготовления 72 кг кураги?
Задание 12.
На клетчатой бумаге с размером клетки 1×1 отмечены точки A и B. Найдите расстояние между этими точками.
Задание 13.
Дан треугольник ABC. Известно, что AB = BC = 25, AC = 40. Найдите синус угла A.
Задание 14.
Укажите номер верного утверждения.
1) Если в параллелограмме две стороны равны, то такой параллелограмм является ромбом.
2) Если в четырёхугольнике две диагонали равны и перпендикулярны, то такой четырёхугольник — квадрат.
3) Если в ромбе диагонали равны, то такой ромб является квадратом.
4) Углы при меньшем основании трапеции тупые.
Задание 15.
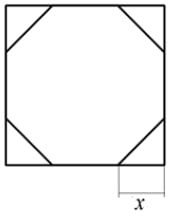
У стекольщика есть квадратное стекло. Сторона квадрата равна 40 см. Нужно вырезать из этого стекла восьмиугольник, у которого все стороны равны и все углы равны. Для этого нужно наметить линии и по этим линиям отрезать от квадрата четыре одинаковых прямоугольных треугольника по углам (см. рисунок). Найдите приближённо длину катета одного такого треугольника в миллиметрах, считая, что √2 равен 1,41.
Запишите решение и ответ.
Задание 16.
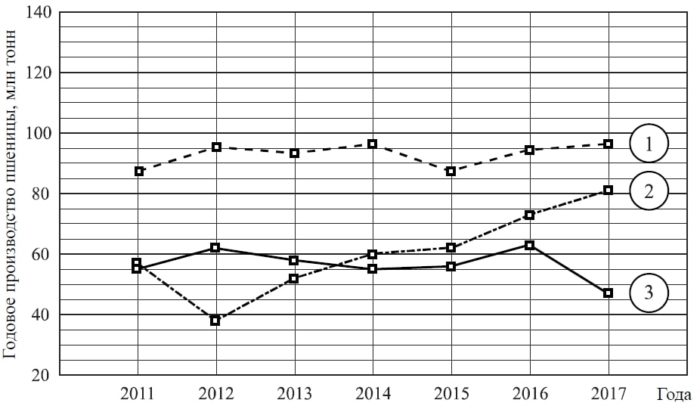
Годовое производство пшеницы – это суммарная масса всех сортов пшеницы, выращенной в стране в течение года. Обычно измеряется в млн тонн. На диаграмме показано производство пшеницы в млн тонн в России, США и Индии за семь лет начиная с 2011 года. Рассмотрите диаграмму и прочтите фрагмент сопровождающей статьи.
В 2012 году на основных хлебородных территориях России случилась аномальная засуха. Она повсеместно нанесла значительный ущерб посевам пшеницы, а на 8% площадей полностью погубила урожай. Погодные условия мешали не только российским хлеборобам.
В 2015 году в Индии длительная жара привела к выгоранию части площадей, занятых пшеницей. Кроме того, на урожайности пшеницы в Индии в том году негативно сказались чрезмерные осадки и град, последовавшие за засухой.
В США из-за падения закупочных цен на пшеницу в 2017 году фермеры сократили на 1,5 млн га посевные площади, отведённые под пшеницу. Засуха и поздние метели в США в том же году стали причиной рекордно низкой урожайности зерновых.
В Китайской Народной Республике в большинстве хлебородных районов на протяжении последних десяти лет погода благоприятствовала сельскому хозяйству. Постепенно повышающаяся культура земледелия в КНР способствует небыстрому устойчивому росту производства пшеницы, составляющей наряду с рисом основу рациона населения. В 2015 году урожай составил 130 млн тонн – на 10 млн тонн больше, чем четырьмя годами раньше. Однако 2016 год оказался менее удачным и суммарный урожай снизился на 2 млн тонн по сравнению с 2015 годом. Но уже в 2017 году снова наблюдался резкий рост по сравнению с прошлым годом, а суммарный урожай пшеницы в 2017 году оказался на 10% выше, чем в 2011 году.
1) На основании прочитанного определите, какой стране соответствует каждый из трёх графиков.
2) По имеющемуся описанию постройте схематично график производства пшеницы в Китае в 2011–2017 гг.
Задание 17.
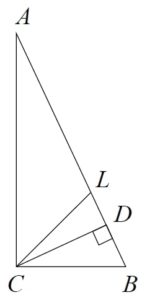
В прямоугольном треугольнике ABC с гипотенузой AB провели высоту CD и биссектрису CL. Найдите величину угла DCL, если ∠CAB = 25°. Ответ дайте в градусах. Запишите решение и ответ.
Задание 18.
Расстояние между пунктами А и В по реке равно 45 км. Из А в В одновременно отправились плот и моторная лодка. Моторная лодка, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 28 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.
Запишите решение и ответ.
Задание 19.
Сумма ста натуральных чисел равна 5000. Все эти числа разбили на три группы, причём во всех группах разное количество чисел. Известно, что:
– в первой группе 29 чисел, их среднее арифметическое равно 21;
– среднее арифметическое чисел второй группы равно 50;
– среднее арифметическое чисел третьей группы – целое число.
Найдите количество чисел в третьей группе.
Запишите решение и ответ.
Источник варианта: fioco.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.5 / 5. Количество оценок: 11
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.